【数学の疑問】なぜ確率は掛け算なのか?3つの考え方を紹介!例題を解きながら解説します

確率は中学生、高校と難易度は違うものの扱う単元となります。大学に入っても扱うことがあるので大切な単元であるといえます。身近な確率でいうと野球の打率、天気予報などがありますね。
問題文を見てみよう
例えば以下のような問題があったとします。
問題文「ある日の翌日は、晴れ0.5、曇り0.3、雨0.2の確率でそれぞれの天気になるとします。」
問1 「この時、二日連続で晴れになる確率は?」
これは、0.5×0.5=0.25だから0.25だ!と言われて納得いくでしょうか?
あるいは以下のような問いがあったとします。
問2 「この時、翌々日が晴れになる確率は?」
これは、(0.5×0.5)+(0.3×0.5)+(0.2×0.5)=0.5だ!と言われて納得いくでしょうか?
確率は掛け算だと習ったのになんで足し算をするんだと思ったでしょうか。
これらの疑問について問1、問2を解くための考え方を説明する中で納得して頂けたら幸いです。
【問1】二日連続で晴れになる確率は?
まず問1について解いていきます。
一般的な説明としては視覚的にも分かりやすいので樹形図を使う説明が最も多いです。
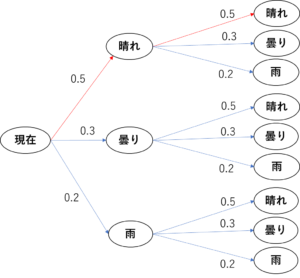
上の図を見ながら考えていきます。
「現在」から「晴れ」になるのは0.5だと与えられているので確率は0.5です。
「晴れ」から「晴れ」になるのは0.5の確率なので、0.5×0.5=0.25となります。
これだけでは納得いかないという方には直感的にこの確率を理解する考え方として2つ提案したいと思います。
ピザを切り分けるように考える
大きさ1のピザを切り分けてみましょう。

晴れの部分のピザを別のお皿に入れます。
形を整えると大きさ0.5のピザができます。
こちらも同じように天気の確率でピザを分けることができます。
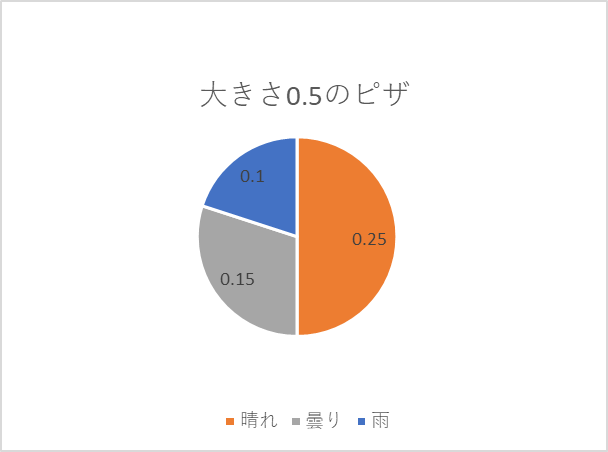
この時の「晴れ」の部分を見ると0.25の大きさであることが分かります。
確率は状態であるという考え方
そもそも確率とは何なのでしょうか。
様々な説明の仕方があると思いますが、一つの考え方として状態であるといえます。
このような前提に立った時、問題を解く前の状態はどうでしょうか。
何もしていないのであらゆる可能性は存在する、つまりどのような状態も許容する状態であるといえます。
この状態を1とするのが確率の考え方です。
このように考えると問題を解く前の状態を解くまで続けているともいうことができます。
計算で考えると1×1×1×1×…とずっと続いているということです。
そして、問題を解くことで状態が分岐していきます。
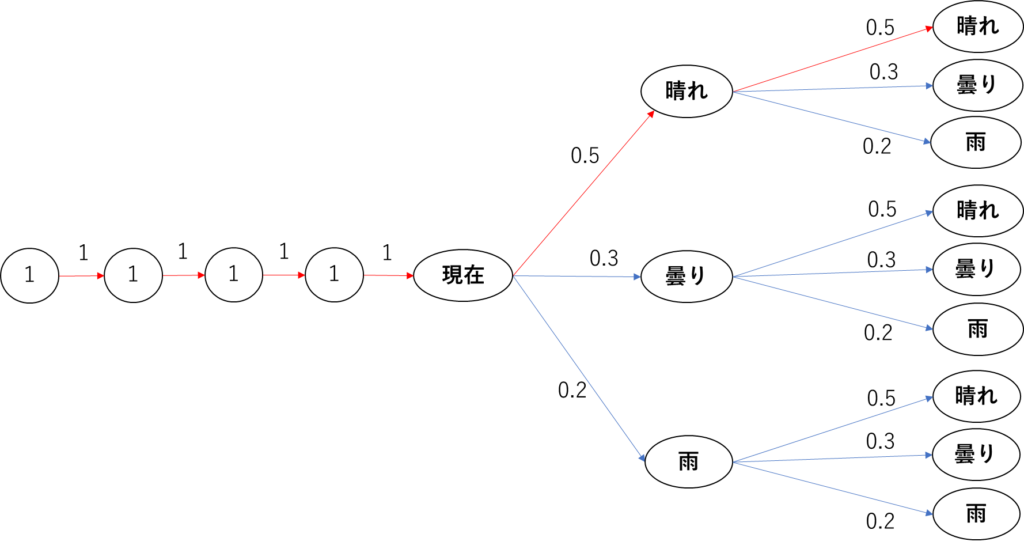
「現在」→「晴れ」の確率は1×1×1×…×1×0.5=0.5です。
「現在」→「晴れ」→「晴れ」の確率は 1×1×1×…×1×0.5 ×0.5=0.25です。
このように状態で確率を考える方法もあります。
【問2】翌々日が晴れになる確率は?
では問2についてもそれぞれの考え方に基づいて解いてみましょう。
樹形図を使うのが一般的でしたね。
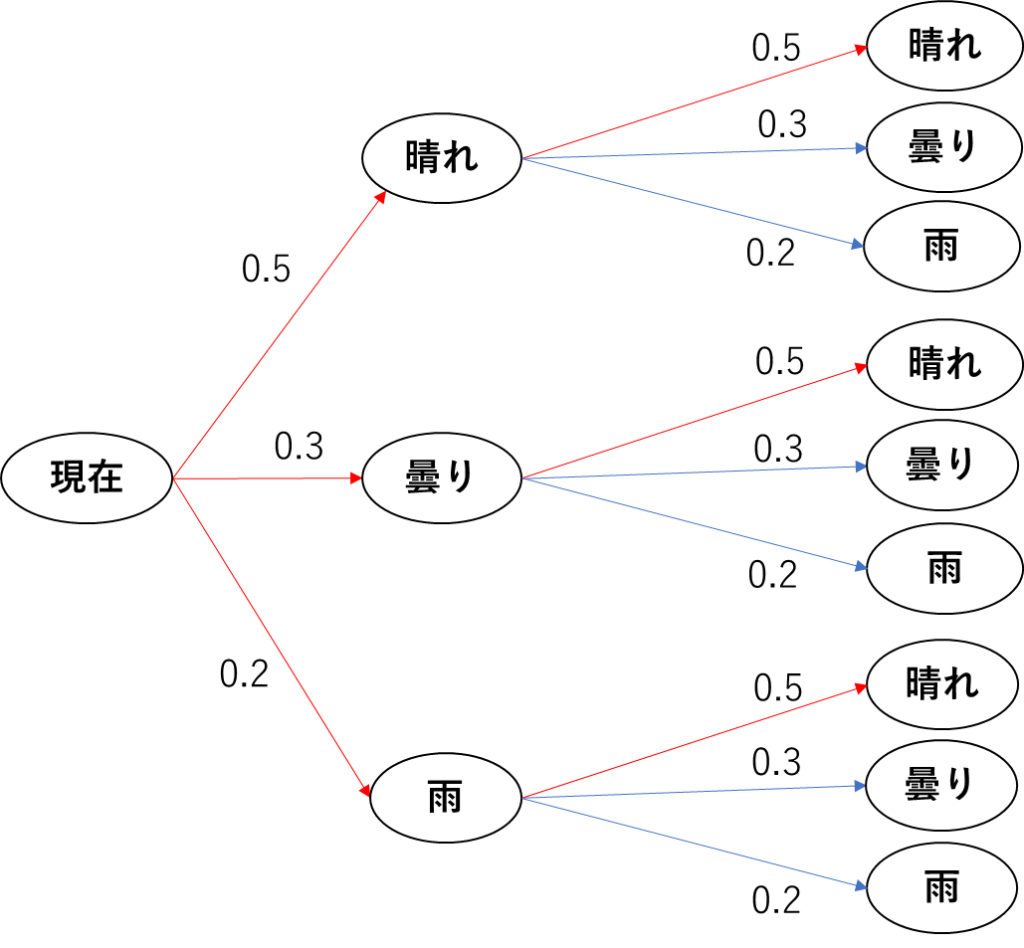
(0.5×0.5)+(0.3×0.5)+(0.2×0.5)=0.5 です。
ピザを切り分けるように考える
ピザを分けてみましょう。
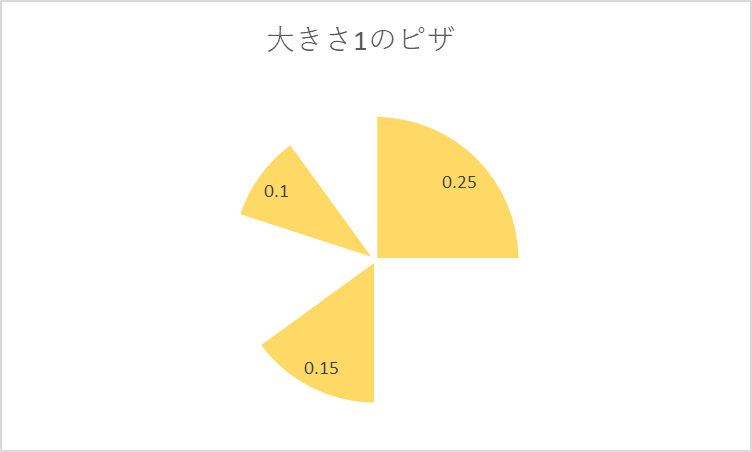
残ったピザは0.25+0.15+0.1=0.5です。
確率は状態であるという考え方
状態は続いているので以下のような樹形図になります。
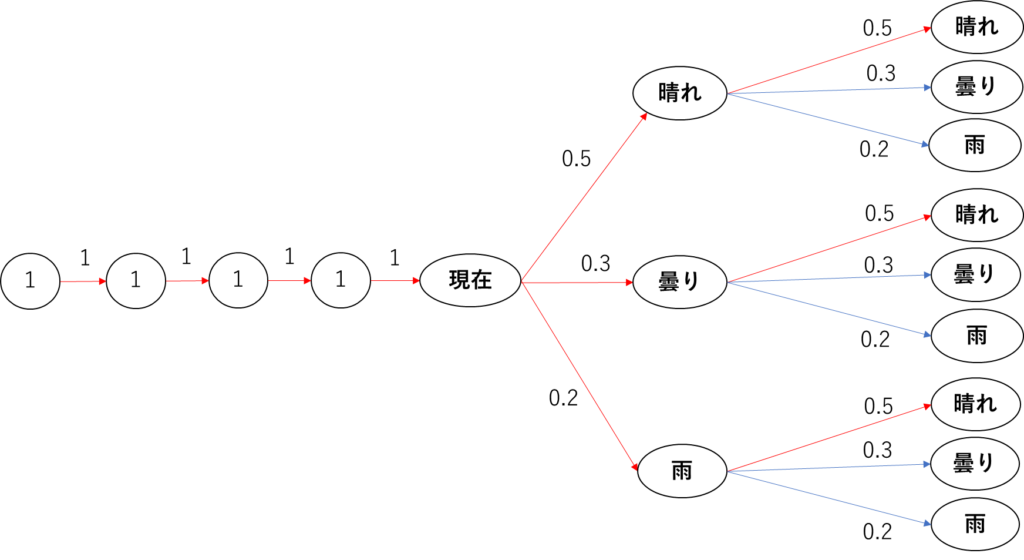
翌々日が晴れになっている状態は以下の三つです。
「現在」→「晴れ」→「晴れ」の確率は 1×1×1×…×1×0.5 ×0.5=0.25
「現在」→「曇り」→「晴れ」の確率は 1×1×1×…×1×0.3 ×0.5=0.15
「現在」→「雨」→「晴れ」の確率は 1×1×1×…×1×0.2 ×0.5=0.1
分岐した状態を足すと0.5です。
最後に
いかがだったでしょうか。
個人的には 「確率は状態であるという考え方」が気に入っています。
今回は三つの考え方について説明してきましたが、これらの考え方にとらわれずに自分自身の納得のいく考え方を見つけてもらえたら幸いです。
視点を変えて確率が掛け算で求められる理由を知りたい方はこちらをご覧ください。
マイナス同士の掛け算がプラスになるのはなぜ?



コメント