【Pytorch】nn.Dropoutの引数・使い方・挙動を徹底解説!要素の一部を確率pでゼロにする方法

nn.Dropoutは、訓練中にランダムに一部のニューロンの活動を無効化(ゼロにする)ことで、ネットワークが特定のニューロンの存在に依存しすぎることを防ぎます。これは、ニューラルネットワークがデータの特性をより一般的に捉え、新しいデータに対する予測性能を向上させるのに役立ちます。
torch.nn.Dropout — PyTorch 2.0 documentation
torch.nn.functional.dropout — PyTorch 2.0 documentation
イメージを掴もう
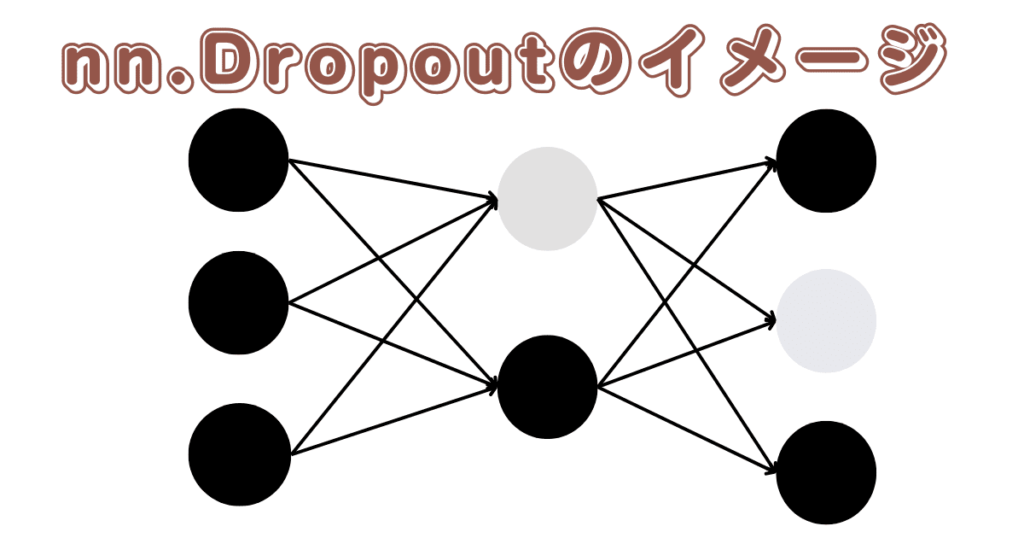
nn.dropoutの引数
- p (float)
ゼロにする確率を表すパラメータです。
デフォルト値は0.5です。 - inplace (bool)
Trueに設定すると、操作をインプレース(元のテンソルを変更)で行います。
デフォルト値はFalseです。
nn.Dropoutの使い方
簡単にドロップアウトを実装できます。
import torch
import torch.nn as nn
# ドロップアウト確率0.2のnn.Dropoutを定義
dropout = nn.Dropout(p=0.2)
# 入力テンソルを作成
input_tensor = torch.tensor([1, 2, 3, 4, 5], dtype=torch.float32)
# ドロップアウトを適用
output = dropout(input_tensor)nn.Dropoutの挙動
ニューラルネットワークを想像するとき、それはたくさんのニューロン(またはノード)が互いにつながって学習するシステムだと考えられます。
ドロップアウトは、学習中にランダムに一部のニューロンを「オフ」にする方法です。これにより、ネットワークはすべてのニューロンに依存せずにデータを学習できます。
具体的には、指定された確率p(例えば、0.5なら50%の確率)で、入力された情報の一部を無視(ゼロにする)します。これは各ステップごとにランダムに行われ、全ての「チャネル」(情報の流れ)がそれぞれ独立して処理されます。これが有用な理由は、ネットワークが学習する際に「共同適応」を防ぐことができるからです。共同適応とは、ある特定のニューロンが特定の他のニューロンに過度に依存してしまい、他のニューロンが不要になってしまう現象を指します。ドロップアウトを使用することで、これを防ぎ、ネットワーク全体がより均等に学習できるようになります。
最後に、ドロップアウトは訓練時だけに適用され、評価(テスト)時には適用されません。そのため、訓練時に無視された情報も、評価時にはフルに利用されます。これを補うために、訓練時には活性化されたニューロンの出力を強化(各要素をp/1-p倍する)します。これにより、訓練時と評価時での振る舞いの違いを緩和します。
上記の説明では分からない部分もあると思うので挙動をみてみましょう。
p=0.2の場合
import torch
import torch.nn as nn
# ドロップアウト確率0.2のnn.Dropoutを定義
dropout = nn.Dropout(p=0.2)
# 入力テンソルを作成
input_tensor = torch.tensor([1, 2, 3, 4, 5], dtype=torch.float32)
# ドロップアウトを適用
output = dropout(input_tensor)
print("入力テンソル:", input_tensor)
print("ドロップアウト適用後の出力:", output)単純にp=0.2を指定しています。
何回か出力してみます。
# 1
入力テンソル: tensor([1., 2., 3., 4., 5.])
ドロップアウト適用後の出力: tensor([0.0000, 2.5000, 3.7500, 5.0000, 6.2500])
# 2
入力テンソル: tensor([1., 2., 3., 4., 5.])
ドロップアウト適用後の出力: tensor([1.2500, 2.5000, 3.7500, 5.0000, 6.2500])
# 3
入力テンソル: tensor([1., 2., 3., 4., 5.])
ドロップアウト適用後の出力: tensor([1.2500, 0.0000, 3.7500, 5.0000, 6.2500])このようにp=0.2を指定したからといってテンソル内の2割の要素が必ず0になる訳ではありません。
また、この結果から各要素が1/(1-p)倍になっているのが確認できます。今回はp=0.2なので1.2倍になっています。
inplace=Trueの場合
import torch
import torch.nn as nn
# ドロップアウト確率0.5でインプレース操作を行うnn.Dropoutを定義
dropout = nn.Dropout(p=0.5, inplace=True)
# 入力テンソルを作成
input_tensor = torch.tensor([1, 2, 3, 4, 5], dtype=torch.float32)
# ドロップアウトを適用
output = dropout(input_tensor)
print("入力テンソル:", input_tensor)
print("ドロップアウト適用後の出力:", output)inplace=Trueとすると元のテンソルも変化します。
入力テンソル: tensor([ 2., 0., 0., 0., 10.])
ドロップアウト適用後の出力: tensor([ 2., 0., 0., 0., 10.])2次元のテンソルの場合
import torch
import torch.nn as nn
# ドロップアウト確率0.5のnn.Dropoutを定義
dropout = nn.Dropout(p=0.5)
# 2次元の入力テンソルを作成
input_tensor = torch.tensor([[1, 2, 3], [4, 5, 6]], dtype=torch.float32)
# ドロップアウトを適用
output = dropout(input_tensor)
print("入力テンソル:")
print(input_tensor)
print("ドロップアウト適用後の出力:")
print(output)2次元のテンソルについても同じように用いることができます。
# 1
入力テンソル:
tensor([[1., 2., 3.],
[4., 5., 6.]])
ドロップアウト適用後の出力:
tensor([[ 2., 0., 0.],
[ 0., 0., 12.]])
# 2
入力テンソル:
tensor([[1., 2., 3.],
[4., 5., 6.]])
ドロップアウト適用後の出力:
tensor([[2., 0., 0.],
[8., 0., 0.]])
# 3
入力テンソル:
tensor([[1., 2., 3.],
[4., 5., 6.]])
ドロップアウト適用後の出力:
tensor([[ 0., 4., 6.],
[ 8., 10., 12.]])nn.Dropoutを使わずにドロップアウトを実装する
実装というほどではないですが、nn.Moduleを継承したドロップアウトを作成しました。
import torch
import torch.nn as nn
class CustomDropout(nn.Module):
def __init__(self, p=0.5):
super(CustomDropout, self).__init__()
self.p = p
def forward(self, x):
if self.training:
# トレーニングモードの場合、ドロップアウトを適用する
# マスクを作成し、各要素をドロップアウトする確率でサンプリングする
mask = torch.empty_like(x).bernoulli_(1 - self.p)
# ドロップアウトされた要素を0にセットし、保持する要素はスケーリングする
x = x * mask / (1 - self.p)
# テストモードの場合やドロップアウトが適用されない場合は入力をそのまま返す
return x
実行速度など色々と劣っていると思いますが動作はしています。
import torch
import torch.nn as nn
# ドロップアウト確率0.5のnn.Dropoutを定義
dropout = CustomDropout(p=0.5)
# 多次元の入力テンソルを作成
input_tensor = torch.tensor([[1, 2, 3], [4, 5, 6]], dtype=torch.float32)
# ドロップアウトを適用
output = dropout(input_tensor)
print("入力テンソル:")
print(input_tensor)
# 入力テンソル:
# tensor([[1., 2., 3.],
# [4., 5., 6.]])
print("ドロップアウト適用後の出力:")
print(output)
# ドロップアウト適用後の出力:
# tensor([[ 2., 0., 0.],
# [ 0., 10., 12.]])まとめ
nn.Dropoutは、入力テンソルの一部の要素を確率pでランダムにゼロします。
また、それぞれの要素をp/(1-p)倍します。


コメント